The classical way of inscribing a regular pentagon in a circle is discussed in Book IV, Proposition 11 of Euclid’s Elements. The method of Euclid is a bit complicated since it requires first to draw a golden triangle (a 72-72-36 triangle) and then to inscribe the triangle in the given circle.
In this post I want to describe the method I like to use. This method is based on a method described in the book “The Glorious Golden Ratio” by Alfred S. Posamentier and Ingmar Lehmann. Their method is slightly more complicated because they show how the golden ratio is embedded in the yin and yang symbol.
A Circle Inside a Circle
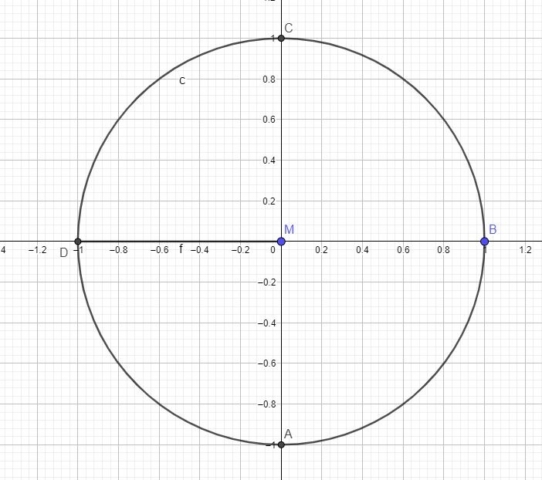
We can start with a circle with center M and radius R=1. Then you have to construct 2 perpendicular diameters (or 2 perpendicular lines that meet at M). For convenience, you can work in Geogebra and make M the point (0,0). Then you can use the x and y lines as the perpendicular lines that meet at M. A and C are the intersection between the y line and the circle. B and D are the points of intersection between the x line and the circle. Figure 1 shows the initial unit circle.
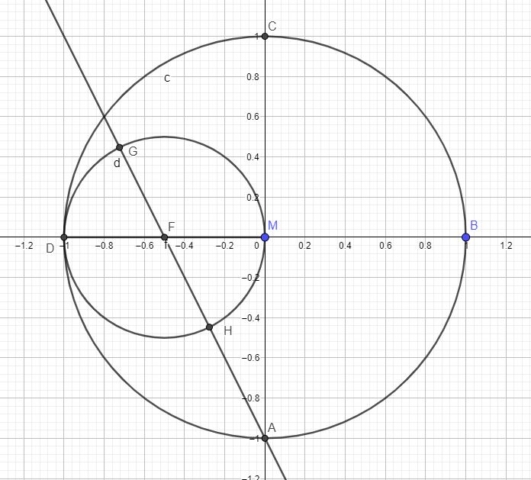
The next step is to draw the point F that is the midpoint of DM. Next you draw the circle centered at F and with the radius FM. Now draw the line that passes though A and F. This line will intersect the circle centered at F at the points G and H. Figure 2 shows the construction.
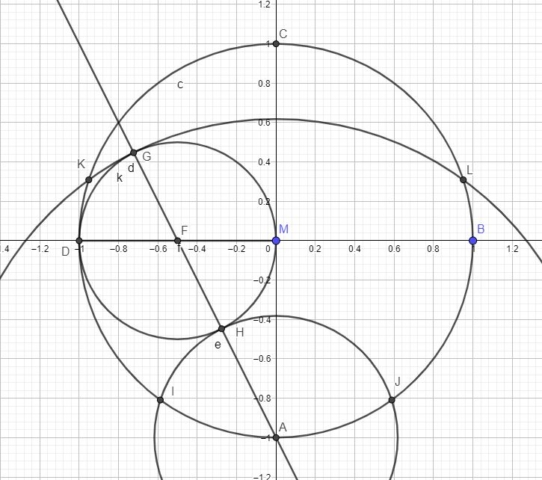
Now we draw a circle centered at A and with the radius AH. This circle will intersect the original unit circle at I and J. Next we draw another circle centered at A and with the radius AG. This circle intersects the original circle at K and L. Figure 3 shows the steps.
The only thing that remains is to connect the points I, J, L, C and K to obtain the regular pentagon IJLCK. Figure 4 shows the pentagon.
Golden Ratio
The pentagon and the pentagram has many connections with the golden ratio φ= 1.61803…, so its not surprising if we find the golden ratio in the constructions presented above. The golden ratio is already present in Figure 2, because the magnitude of AG is the golden ratio. This means that AG=AK=AL=1.61803…. We also have AH=AI=AJ=1/φ =φ-1 = 0.61803… (the inverse of the golden ratio).
In the book “The Glorious Golden Ratio” the authors slightly complicate the drawing because they draw 2 semicircles inside the unit circle instead of drawing just one circle (the circle centered at F). They draw 2 semicircles to create a yin yang symbol. One semicircle can point upwards and be centered at F. The other semicircle points downwards and it is centered at the midpoint of MB.
I think that it is quite interesting that the pentagon and the yin yang symbol are connected to each other. By extension, the pentagram is also connected to the yin yang symbol. The link between all of them is provided by the golden ration.
People interested in golden ratio constructions should also read my post about the hexagram and the golden ratio. The post is also based on a drawing from “The Glorious Golden Ratio” book.