Many people that are familiar with the golden ratio ( Φ = 0.5(1+ 50.5) which is about 1.61803), know that it appears very often in the proportions of the pentagon and the pentagram. In this post I want to present a diagram that connects the golden ratio with the regular hexagram or the six pointed star (also known as the Star of David).
The diagram is taken from “The Glorious Golden Ratio” by Alfred S. Posamentier and Ingmar Lehmann. The diagram is discussed on pages 197-199 [1].
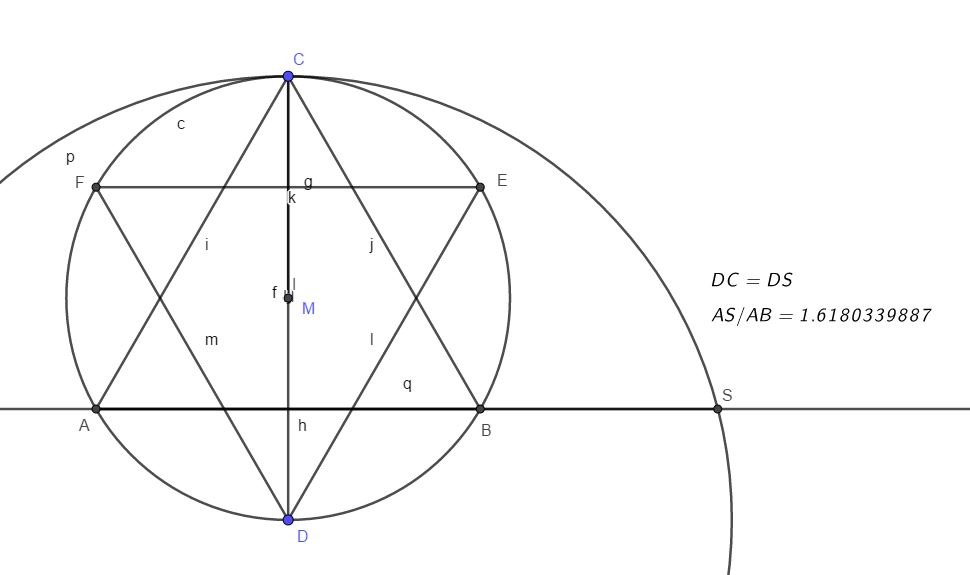
Golden Ratio Diagram
In the image above, the point B partitions the segment AS in the golden ratio. Thus, AS/AB is about 1.618033. The points A and B are two vertices of the regular hexagram. The point S is at the intersection of the line passing through the points A and B and the circle centered at D and with the radius equal to CD.
In the book [1], the authors provide a detailed proof of the diagram. I will let the readers try to prove that the proportion AS/AB is indeed the golden ratio or the golden segment.
Hexagram Construction
Let’s go a little bit over the construction of a regular hexagram. Overall, the construction of a regular hexagram is almost the same as the construction of a regular hexagon. In our diagram, ADBECF is a regular hexagram.
In GeoGebra I started with the point M located at the origin (0,0) and point C at (0,1). Then you can draw the circle centered at M and with the radius r=MC. A line that passes through C and M will meet the circle at point D. The segment CD is a diameter of the circle centered at M. The points E and F are the intersections of the circle with center at M and the circle centered at C and the same radius r=CM. The points A and B are the intersection of the circle M and the circle centered at D and with the radius r=DM=CM (you cannot see the additional circles in the diagram above). After you obtain the Points A,B,C,D,E and F you can connect them in a hexagram.
All the steps above use the fact that the radius r of the circle circumscribing a regular hexagon, is equal to the sides of the hexagon. In our diagram CM=r= AD=DB=BE=EC=CF=FA. In our case I used a unit circle with r=1. Using the radius r and an initial vertex, you can easily find the location of the other five vertices.
In the steps above I used coordinates to make things more easier. But besides the use of the coordinates, the steps are similar to the steps used in Proposition 15 from Book 4 of Euclid’s Elements (see this online version) [2]. The fact that the radius of the circumscribing circle is equal to the sides of the hexagon is a corollary or porism of Prop. 15 from Book 4.
Trivia
A hexagram appears in the famous painting “The School of Athens” by Raphael. A geometrician in the painting, most likely Euclid, is drawing a hexagram on a tablet. The scene is depicted on the bottom right of the painting. See this article for more details [3].
Sources
[1] “The Glorious Golden Ratio” by Alfred S. Posamentier and Ingmar Lehmann,p197-199
[2] Euclid’s Elements Book 4 Proposition 15
[3]Haas, R. “Raphael’s School of Athens: A Theorem in a Painting?,” Journal of Humanistic Mathematics, Volume 2 Issue 2 (July 2012), pages 2-26. DOI: 10.5642/jhummath.201202.03 . Available at:
https://scholarship.claremont.edu/jhm/vol2/iss2/3

1 comment