In my previous blog post about trisection “Angle Trisection: a Neusis Construction using Lill’s Method and Lill’s Circle”, I showed a “mechanical” method for trisecting an angle smaller than 90 degrees. The neusis construction involved the Lill’s method representation of cubic equations of the form x3 -3tan(θ)x2 -3x + tan(θ). These cubic equations have 3 real roots. One of the roots is equal to tan( θ/3), which also gives the solution to our trisection problem.
A neusis construction is always an approximation. In this post I want to show how to obtain an exact solution using a hyperbola. I will use the same Lill’s method representation of cubic equations of the form x3 -3tan(θ)x2 -3x + tan(θ). However, this time we will intersect Lill’s circle with a hyperbola that can be easily generated in GeoGebra.
I also want to mention that I will not provide proofs, so many of the techniques or statements made in this post should be treated as conjectures.
A Specific Example
In my neusis post I showed a general way of representing x3 -3tan(θ)x2 -3x + tan(θ) using Lill’s method. For convenience , in this post I will let tan(θ)=2, so we will deal with the cubic polynomial x3 -6x2 -3x + 2. I will represent the polynomial using the method described in this post, so the solutions to the cubic equations are on the x-axis.
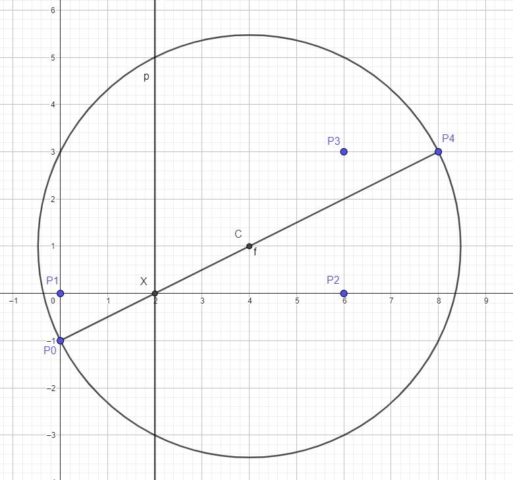
In the image below you can see the initial Lill method setup. The polynomial equation is represented by the path P0P1P2P3P4, where P0P1=1, P1P2=-6, P2P3=-3 and P3P4=2. Point C is the midpoint of P0P4, and it is the center of Lill’s Circle.
Point X is the intersection between the x-axis and the segment P0P4. At point X I also constructed a perpendicular line to the x-axis. If you read neusis article, the setup should be familiar.
Trisection Hyperbola and Lill’s Circle
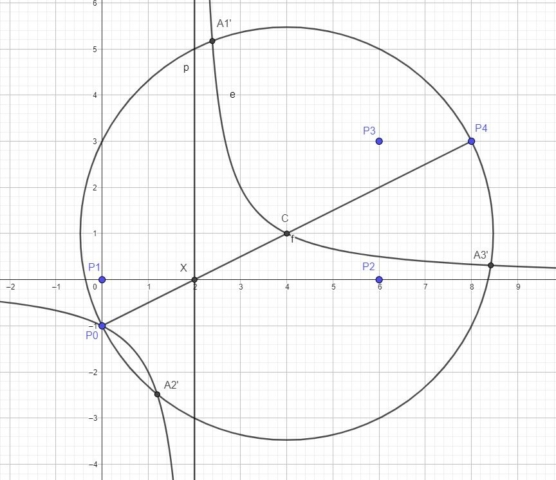
The roots of the polynomial can be obtained by intersecting Lill’s circle with the hyperbola that has P0 as one of its points and whose asymptotes are the x-axis and the perpendicular to the x-axis at X.
This hyperbola will intersect Lill’s circle at the points P0, A1′,A2′ and A3′. This hyperbola also passes trough point C (which is the reflection of point P0 about point X). The hyperbola is shown in the image below.
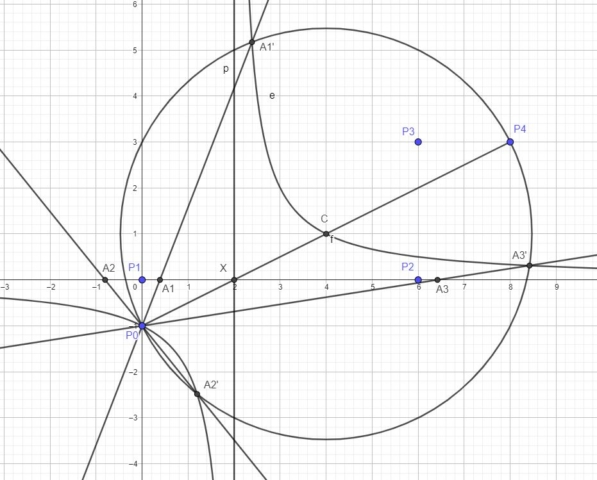
To obtain the roots of the polynomial equation, we simply intersect the lines P0A1′, P0A2′ and P0A3′ with the x-axis. The roots are given by the points A1, A2 and A3 as shown below.
If we let m(P1P0P4)=θ, then m(P1P0A1)=θ/3 (due to the rules of Lill’s method, θ is actually negative in this case). Also P1A1= -tan( θ/3) (which is a positive value and equal to the x-coordinate of point A1).
Constructing the Trisection Hyperbola
GeoGebra needs 5 points to construct a general conic section. In this case we know that the points P0 and C are on the hyperbola. We also know that the asymptotes of the hyperbola are the x-axis and and the perpendicular at X to the x-axis. So we need to generate 3 more points.
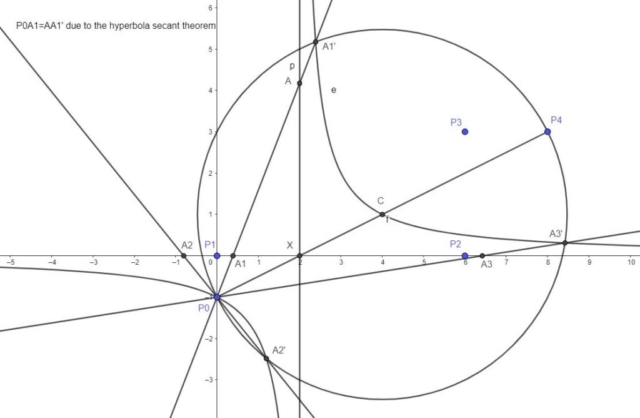
To generate more points we can use the following theorem: On any secant of an hyperbola, the segments between the curve and the asymptotes are equal. For more details about the “Hyperbola Secant Theorem” see this The Encyclopædia Britannica page.
If we let A be the intersection between the line P0A1′ and the perpendicular at X, then P0A1=AA1′ due to the hyperbola secant theorem. Of course, we initially don’t know the location of A1′, A2′ or A3′, so we need to draw random secant lines passing through P0 or C. Using the hyperbola secant theorem you can generate 2 additional points. The 5th point can be generated by reflecting one of the newly discovered points about the point X (as I mentioned above, the point C and P0 are the reflection of each other about point X).
In my neusis post I mentioned that the trisection occurs when certain segments are equal. The notation in that post was a bit different, but the 2 segments were equivalent to P0A1 and AA1′. Now we know that the 2 segments are equal because of the properties of hyperbolas.
Trisection Hyperbolas, Equilateral Triangles and Lill’s Circle point Projections
The trisection hyperbolas that provide the solutions to our trisection problem and also find the roots of the polynomials of the form x3 -3tan(θ)x2 -3x + tan(θ) seem to have other interesting properties. The trisection hyperbolas can be considered as circumconics passing through the points A1′, A2′ and A’3. The points A1′, A2′ and A3′ can be considered as projections from point P0 onto the Lill’s circle of the root points A1, A2 and A3.
The points A1′, A2′ and A3′ are special because they always seem to form an equilateral triangle. Thus the 3 points seem to form an equilateral triangle inscribed in Lill’s circle. Also the trisection hyperbola may qualify as a Kiepert Hyperbola, Feuerbach or other type of circumconic hyperbola. The trisection hyperbola is a rectangular hyperbola that passes through the vertices of an equilateral triangle, so it may qualify as a special case of some of these circumconic hyperbolas.
Angle Division and Inscribed Regular Polygons
The polynomial family x3 -3tan(θ)x2 -3x + tan(θ) was obtained using the triple angle tangent formula illustrated below. This polynomial family always has 3 roots and the root with the smallest absolute value is tan( θ/3).
We can obtain similar families of polynomials that have tan(θ/n) as a root. The polynomials can be obtained using the following multiple-angle tangent formula
The polynomial that deals with angle quintisection is x5 -5 tan(θ) x4-10 x3 +10 tan(θ) x2 +5 x – tan(θ). If we project the roots of 5th degree polynomial onto the Lill’s circle the same way we did to the cubic equation, the 5 points projected onto Lill’s circle seem to describe a regula pentagon inscribed inside Lill’s circle.
So the roots of polynomials obtained using the multiple-angle tangent formula seem to form regular polygons inscribed inside Lill’s circle when we do Lill’s Circle Projections. I may discuss this topic further in future posts.
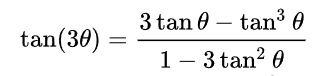
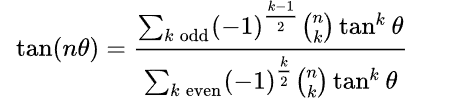
1 comment