The problem of trisecting an angle using just a compass and a straightedge is an impossible problem. However, the problem of angle trisection can be solved if we are allowed the use of a marked ruler. Geometric constructions that use a marked ruler are called neusis constructions. You can learn more about the topic of neusis construction by reading the dedicated wikipedia page.
In this post I want to show a new neusis construction to the angle trisection problem. This is a construction that I discovered recently, but it may be similar to other neusis constructions that I am not aware of (this problem is very old after all, and many people tried their luck at cracking the trisection problem). I should also add, that my construction deals only with angles less than 90 degrees.
My method is connected to Lill’s Method because it can also be used to solve a specific class of cubic equations. You don’t need to know about Lill’s method to follow my construction, but I recommend this page if you want to learn about this visual method. After I introduce my neusis construction, I will provide more context on how this construction is connected to Lill’s method and cubic equations.
Angle Trisection
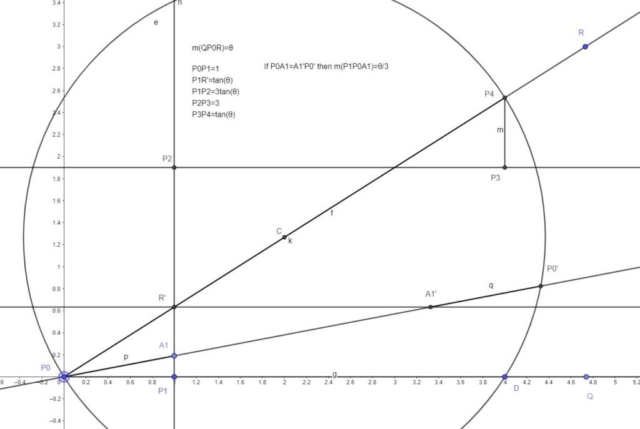
I tried to include all the details of the neusis construction in the image below. We start with the angle m(QP0R)= θ. For convenience, I put the ray P0Q on the x-axis. The point P1 is on P0Q and P0P1=1. At P1 we construct a perpendicular line to P0Q. The perpendicular line meets P0R at R’. P1R’=tan(θ), and we use P1R’ to construct P1P2=3P1R’=3tan(θ). At P2 we construct a perpendicular to the previous perpendicular line (line passing through P1, R’ and P2). On this new line we construct the segment P2P3=3. At point P3 we construct a perpendicular line to the line passing through P2 and P3. This new perpendicular line will meet the line P0R at P4.
The next step is to construct the segment P0P4 and find the midpoint C of this segment. Now we construct the circle with center C and radius r=CP0=CP4. At Point R’ we construct a perpendicular to the line passing through P1 and R’.
Point A1 is a point somewhere on the segment P1R’. Point A1′ is the intersection between the line passing through P0 and A1 and the perpendicular at point R’. Point P0′ is the intersection between the circle centered at C and the line passing trough the P0 and A1. If P0A1=A1’P0′, then m(QP0A1)=θ/3.
Of course, the location of point A1 cannot be found using only a ruler and a compass. This is a neusis construction because we approximate the location of A1 by carefully watching if P0A1= A1’P0′. We need a marked ruler to ensure that the 2 segments are equal. In GeoGebra you can approximate the location of A1 very accurately , since you can zoom for better precision.
Lill’s Circle and Cubic Equations
In my diagram, you can see many perpendicular lines or segments. This is because the path created by P0P1P2P3P4 is actually a Lill’s Method representation of the cubic equation x3 -3tan(θ)x2 -3x + tan(θ). P0P1 represents the coefficient 1, P1P2 represents the coefficient -3tan(θ), P2P3 represents the coefficient -3 and P3P4 represents the coefficient tan(θ).
The segment P1A1 provides the solution to the trisection only when the segment P1A1 is equal to one of the roots of the cubic equation. To be more precise, P1A1 should equal to tan( θ/3).
The Circle centered at C is what I call “Lill’s Circle”. Lill’s Circle can be used to find solutions to the quadratic equations (both real and complex). However, this type of constructions, shows that Lill’s Circle plays a role in cubic equations and maybe other higher order polynomials. Regarding cubic equations, it seams that all real roots of cubic equations can be found in a similar way as I described here. All real cubic roots seem to involve Lill’s Circle and 2 segments of equal size.
In the future I will show a similar neusis construction for finding cubic roots. This method is related to my article about the Lill’s method and the Philo line. My construction will be based on the properties of the Philo line. (see the MathWorld entry and this page that mentions hyperbolas and circles).
After I write the post on cubic roots, I will try to write another post on how similar neusis constructions manifest themselves in all cubic equations (at least regarding the real roots).

1 comment