(Note: This is an article from 2016 that I posted on Hubpages. In this article I used Riaz’s way of illustrating Lill’s method. To become more familiar with Lill’s method I recommend going through the links provided in my Lill’s Method page. Also see my Papers page and my Lill’s method articles/posts. )
In this hub I want to show that the problem of finding the Philo line for a right angle is equivalent to finding the solution to a specific type of cubic equations using Lill’s method. These cubic equations have the following form: αz3-β=0, where α and β are the coordinates of the given point P(α,β). But to make myself more clear, first I must define some important terms.
Philo Line
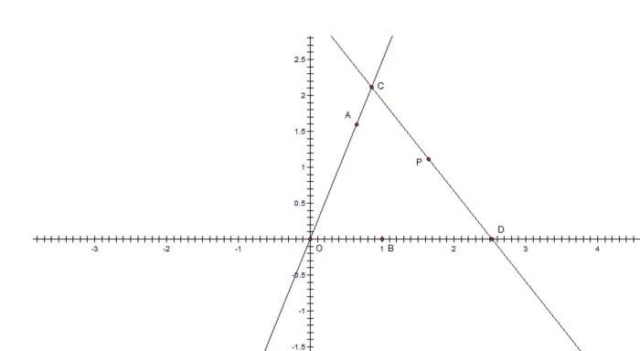
Given two intersecting lines OA and OB forming an angle with vertex at O and a point P inside the angle AOB, the Philo line is the shortest line segment passing though P reaching from line OA to line OB. In image 1, point C is on line OA and point D is on line OB such that the segment CD passes through point P. The segment CD is called a Philo line only if the length of CD has the smallest possible value. Philo line has many interesting characteristics that I will not cover in this hub. Also in this hub I will deal only with the case where mAOB=90.
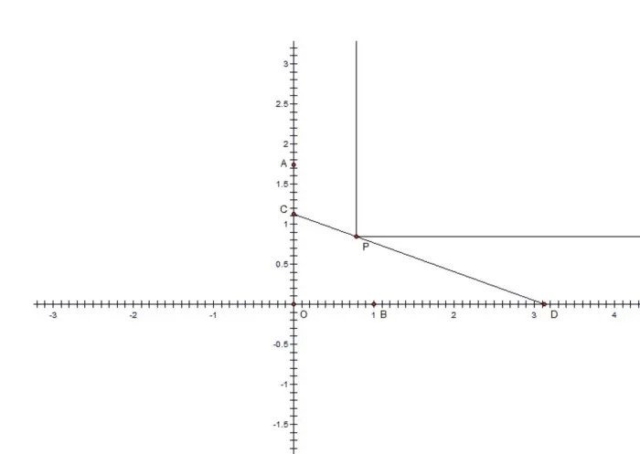
When mAOB=90 , the problem of finding the Philo line can be redefined as another kind of optimization problem. Finding the shortest line through P is equivalent to finding the largest ladder that can fit a corridor with an external corner at O and an internal corner at P. In image 2, the segment CD is a Philo line if it is the longest ladder that can be maneuvered around the corner of the corridor.
If the coordinates of point P are (α,β), where α and β are positive, then the length of the longest ladder that can be maneuvered around the corner of the corridor is given by the formula (α2/3+β2/3)3/2. In this hub I will not prove this formula, but you can see sources [1] and [2] provided at the bottom of this hub.
Cubic Equations and Lill’s Method
In a previous hub I used a specific quadratic equation in order to illustrate some general rules for finding the real roots of a polynomial equation of the form P(z)=anzn+an-1zn-1+…+a1z+a0 using Lill’s method. Lill’s method is very remarkable since the roots of a polynomial can be illustrated geometrically. In Lill’s method, zr is a real root if zr=-tan(θ), where θ is a constant “reflection” or “refraction” angle. It is better to read my previous hub in order to understand Lill’s method.
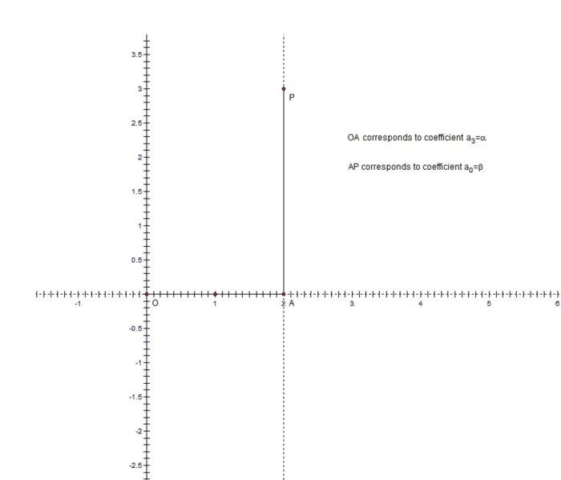
Now let’s have point O(0,0) as the intersection of x and y coordinates. We also start with the point P(α,β), were α and β are positive. Since x and y are perpendicular and α and β are positive, we have a 90 degrees angle and a point P inside it. In the previous section I mentioned the fact that the length of the shortest segment from x to y passing through P(α,β) is (α2/3+β2/3)3/2. Now I want to show how to obtain this formula using Lill’s method.
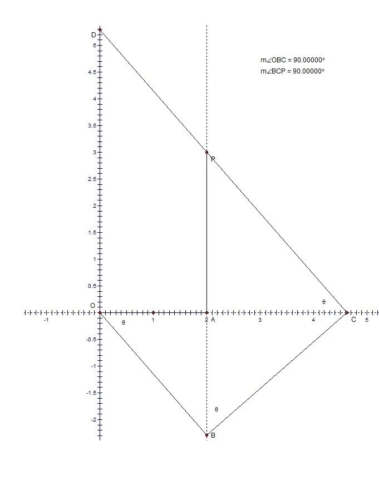
In the introductory paragraph I mentioned the fact that the cubic equation we want to solve using Lill’s method is of the form αz3 -β=0, where α and β are the coordinates of the given point P(α,β). In image 3 I use the length and direction formula akei(n-k)π/2 to construct the reflective segments. In our case a3=α, a2=0, a1=0 and a0=β. The segment OA corresponds to coefficient a3=α and the segment AP corresponds to coefficient a0=β. As explained in my previous hub, all the segments are extended at infinity in both directions by dotted lines and these dotted lines are refractive lines. a2=0 is represented only by a dotted line that overlaps segment AP and its extension of dotted lines. Similarly a1=0 is represented only by a dotted line that overlaps segment OA and its extension of dotted lines. In image 4 I illustrate exactly what it means to find a solution to our equation. We have point B on dotted line belonging to a2=0, point C on dotted line belonging to a1=0 and point D on y axis. Image 4 shows a solution since we have a path of 3 perpendicular “rays” or segments that start from point O and arrive at point P by making 2 “refractions” at constant angle θ. Numerically the root zr=-tan(θ), and θ should be negative in this case and zr should be positive. Now we want to show that CD is the Philo line passing through P.
Equivalence
Without going into details, we know that a cubic equation of the form αz3 -β=0, where where α and β are positive real numbers, has one positive real solution and 2 complex solutions. The cubic is also equivalent to αz3 = β , z3 = β/α or z = (β/α)1/3. Thus zr= -tan(θ) =(β/α)1/3. Looking at image 4 we see that triangles AOB, ABC and ACP are similar. tan=opposite/ adjacent, thus zr= -tan(θ)=AB/OA=AC/AB=AP/AC. We know that OA=α and AP=β. Using the previous proportions we also get AB=α zr, AC=α zr2 and AP=β=α zr3.
To show equivalence we need to show that length of CD= (α2/3+β2/3)3/2. Looking at image 4 we can see that zr= -tan(θ)=OD/OC. OC=OA+AC=α+ α zr2. OD= zrOC=α zr+ α zr3. Finally we see that CD2 = OC2 + OD2. The final calculations are shown in image 5.
Sources
[1] https://ckrao.wordpress.com/2010/11/07/the-ladder-around-a-corner-problem/
[2] Uncommon Mathematical Excursions: Polynomia and Related Realms pages 142-143


1 comment