Whittaker’s Root Series formula is an interesting method that can be used to calculate the root with the smallest absolute value of a polynomial equation. The formula creates a geometrically convergent infinite series using the determinants of a special class of Toeplitz matrices. These Toeplitz matrices are generated using the coefficients of the polynomial equation.
The Whittaker’s Root Series converges only if the polynomial equation has a unique root with the smallest absolute value (however, the smallest root can have a multiplicity higher than 1). For more details about the method , I recommend reading the book “The Calculus of Observations” by E.T. Whittaker starting with page 120 (Archive link). Also read this brief description from a more modern book.
In the past I used Whittaker’s Root Series formula to obtain interesting infinite series. In 2018 I published the article “Generating k-Pell Infinite Series Using Whittaker’s Formula”. I also recommend my articles hosted on this blog ” Fibonacci Infinite Series and the Negative Powers of the Golden Ratio” and “Pell Infinite Series and the Negative Powers of the Silver Ratio”.
In the papers mentioned above, I applied Whittaker’s formula to second degree polynomials (I also experimented with higher degree polynomials but I did not write papers). However, transcendental numbers cannot be the roots of polynomial equations with a finite degree. This is why in this post I want to show an example of applying the Whittaker’s formula on a Taylor series (which can be thought as an infinite degree polynomial).
1/e and ln(1+x) Taylor Series
Whittaker’s root series formula should work on the Taylor series expansion for ln(1+x). Of course, the Taylor series expansion converges when x is between -1 and 1 (including -1 and 1). If we let x=1/e -1, we get ln(1/e)=-1 (of course, e is Euler’s number). To create a polynomial equation, we just take -1 to the other side of the equal side to create the following infinite “polynomial equation”.
We can apply Whittaker’s formula only if the polynomial has a unique smallest root. Looking at various truncations of the polynomial, it seems that the unique smallest root is always close to 1/e -1. As we add more power terms, the root should converge to the true value of 1/e – 1. So to get an infinite series for 1/e-1, we apply Whittaker’s formula to the infinite “polynomial equation”. After calculating the determinants of the Toeplitz matrices and simplifying the signs, I got the following infinite series for 1/e -1.
Of course, there is the possibility that I made some errors when I calculated the determinants of the matrices (I used an online calculator, but I may have entered the wrong number for some matrix elements) . However, I am pretty confident about the bottom fractions because the numerator numbers belong to OEIS sequence A323339, while the denominator numbers belong to A323340. The sum can be simplified to get rid of top and bottom fractions and eliminate the -1 on both sides. Thus, we get the following series for 1/e.
Final Remarks
I think that the most useful thing about Whittaker’s formula is the possibility of finding interesting infinite series for various mathematical constants. There is a chance that some of the terms of the infinite series belong to one of the OEIS sequences. The method can also be useful for generating new OEIS sequences.
Addendum: OEIS sequences A365594 and A365595
The denominators and the numerators of the series that converges to 1/e are now OEIS sequences. The denominators of the series form sequence A365594. The numerators of the series form sequence A365595.

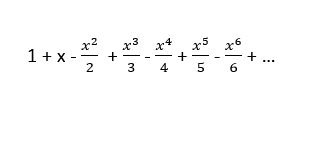


1 comment