In my blog post “Frégier’s Theorem and Frégier Points” I introduced Fregier’s theorem. In this post I want to show an alternative way of constructing or finding the corresponding Fregier points for points on a Parabola. This alternative method makes use of the Vertex point and the parabola’s axis of symmetry.
I am not sure if this method is covered in other math sources. I discovered this method while “playing” in GeoGebra. If anybody knows a source, please comment or send me an e-mail so I can include in this blog post.
Let’s Draw A Fregier Point
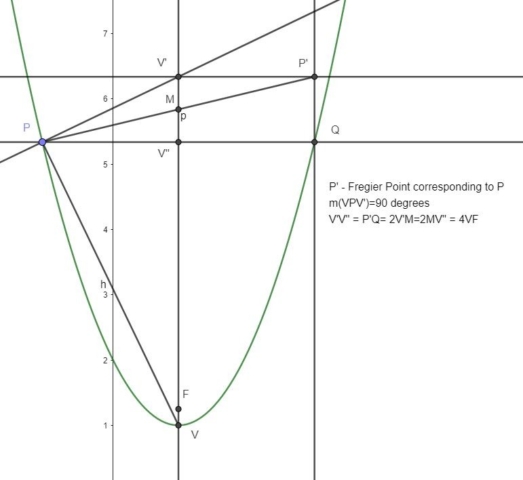
In the image below, V is the vertex of the parabola and P is a point on the parabola. The line passing through V is the axis of symmetry of the parabola and we want to find P’, which is the Fregier point corresponding to P.
We start by constructing the perpendicular to VP at P. This perpendicular line will intersect the axis of symmetry at V’. At V’ we construct the perpendicular to the axis of symmetry. We also construct another perpendicular to the axis of symmetry that goes through P, and this perpendicular will intersect the parabola at Q and the axis of symmetry at V”. The Fregier point P’ is at the intersection of the perpendicular through V’ and the perpendicular at Q to the line passing through P and V” (the perpendicular to the axis of symmetry that goes trough P and V”.
A second option is to construct the point M, which is the midpoint of V’ and V”. The line passing trough P and M will meet the perpendicular trough V’ at P’.
It should be pointed out that this method cannot be used to find the Fregier point corresponding to vertex V.
Some Properties
In the image above I also included a few interesting details. The segments V’V”=QP’= 4 FV (where F is the focus of the parabola).
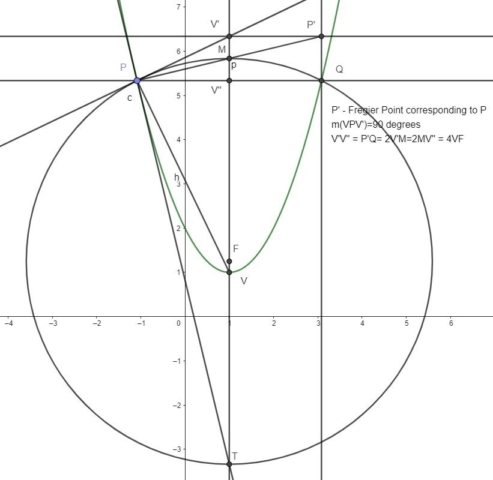
If we draw the circle centered at F with radius r=FP, the circle will pass trough the points M and Q. The circle will also intersect the axis of symmetry at T. The line PT is the tangent to the parabola at P.

1 comment