Due to the properties of the Frégier point, Frégier’s theorem provides a practical means of constructing with straightedge and square the tangent to a conic at any point on the respective conic. Constructing a Frégier point is very easy and the procedure is the same for any type of conic section (parabola, hyperbola, ellipse or circle).
Right now the only online source that gives a more complete overview of Frégier’s theorem is the French Wikipedia page “Point de Frégier”. I believe that none of the sources that I read online go over the special case of rectangular hyperbolas, so I will dedicate a special section for rectangular hyperbolas.
I also want to mention that I discovered an alternative method of constructing Frégier points for parabolas. However, I will not discuss this alternative method in this post since this post is meant to be an introduction to Frégier’s theorem and its application for constructing tangents to conic sections.
Frégier’s Theorem
The definition for Frégier’s theorem (Wolfram MathWorld) [1]:
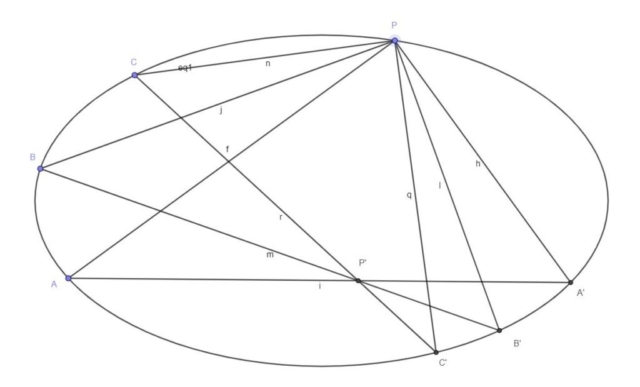
Pick any point P on a conic section, and draw a series of right angles having this point as their vertices. Then the line segments connecting the rays of the right angles where they intersect the conic section concur in a point P’.
In the image above, point P is any point on the conic section (an ellipse in this case). According to Frégier’s theorem, if P is the right angle vertex of the triangles APA’ , BPB’ and CPC’, then the hypotenuses AA’, BB’ and CC’ intersect at the point P’. Point P’ is the Frégier point corresponding to the point P on a conic section.
In the case of a circle, the Frégier point of any point P on the circle is the center of the circle. This is due to Thales’ Theorem. P’ is the center and the hypotenuses AA’, BB’ and CC’ are just diameters of the circle.
Normals and Tangents
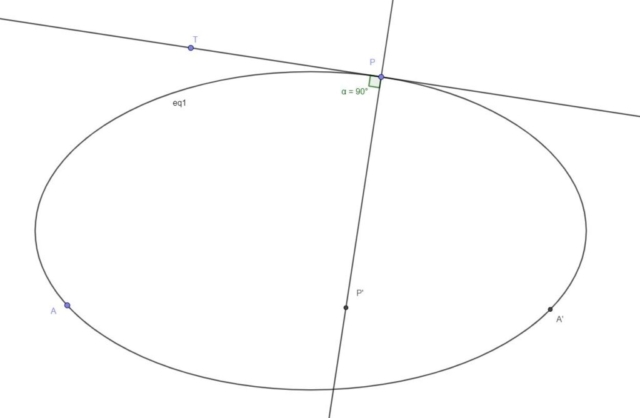
Once you find the corresponding Frégier point P’, it’s easy to construct the tangent to the conic section at the point P. This is because the line through P and P’ is the normal at P. This means that the line passing through P and P’ is perpendicular to the tangent passing through the point P.
So Frégier’s theorem provides a more universal method of creating tangents to points on conic sections. It’s also much easier to create tangents using Frégier’s theorem, since you don’t need the focus points, the vertex, the directrix or any other special points or lines.
Rectangular Hyperbolas
Rectangular hyperbolas are hyperbolas with perpendicular asymptotes. A well known family of rectangular hyperbolas are of the form xy= constant.
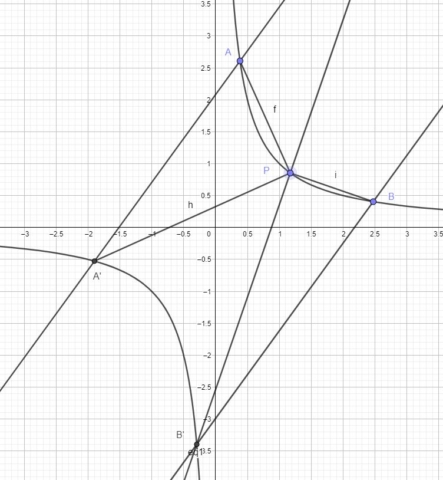
In the case of rectangular hyperbolas the lines passing through AA’, BB’ and CC’ are parallel, so the Frégier point is at infinity. In the image below I omitted the line CC’, but we can see that AA’ and BB’ look parallel.
To construct the tangent at point P, we can simply draw a perpendicular line from P to the lines AA’ or BB’ .

2 comments