The heptagon cannot be constructed with just a ruler and a compass. However, in this post I’ll show how you can construct the heptagon using a hyperbola and the Lill’s circle of a third degree polynomial. The heptagon construction is very similar in nature to my trisection construction that I presented in my “Trisection Hyperbolas and Lill’s Circle” post.
My method involves the Lill’s method representation of the cubic equation x3 + x2 – 2x – 1. The roots of the polynomial can be solved by intersecting the Lill’s circle of the cubic with a specific hyperbola that I will define later. One of the roots of the cubic equations can be used to construct a heptagon.
The Heptagon Cubic Equation
The cubic equation x3 + x2 – 2x – 1 has 3 real roots, but only one is of interest to us. One of the roots is x1= 2cos(360/7). x1 can be used to construct the central angle of a regular heptagon. To better understand the connection between the cubic equation and the heptagon, read this external link.
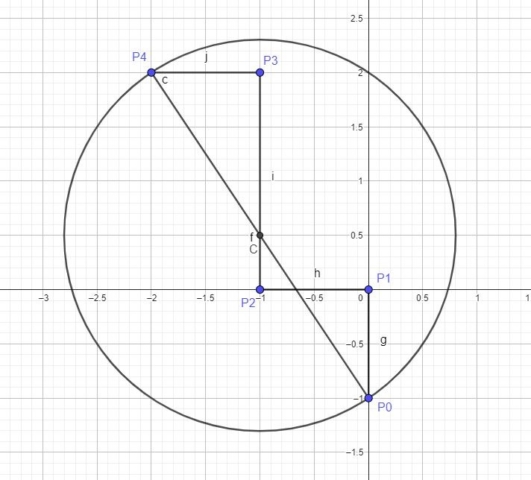
The Lill’s method representation of x3 + x2 – 2x – 1 can be seen in the image below. The Lill representation of the polynomial is represented by P0P1P2P3P4. In the image I also included the Lill Circle with the center at C. The equation of Lill Circle is x2 + y2 +2x-y=2.
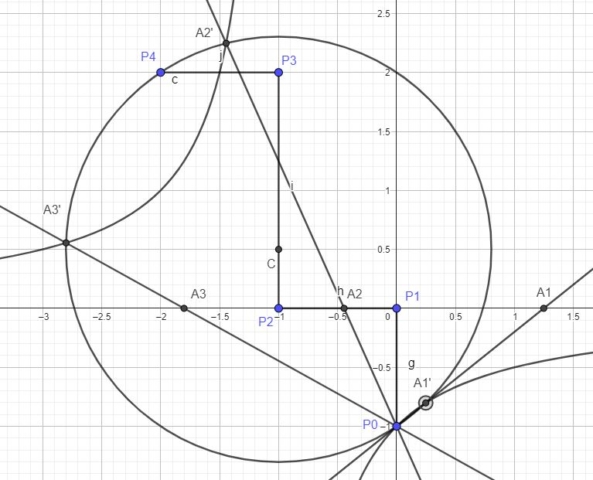
The rectangular hyperbola that can help us find the roots of the cubic equation passes through point P0 and has as asymptotes the x-axis and the line x=-1. The exact equation of the hyperbola is xy+y+1=0. This hyperbola will intersect the Lill circle at the points P0, A1′, A2′ and A3′. The line P0A1′ will intersect the x-axis at A1, the line P0A2′ will intersect the x-axis at A2 and POA3′ will intersect the x-axis at A3. The x coordinates of A1, A2 and A3 are equal to the roots of the cubic equation. Below you can see the hyperbola and the relevant points added to the previous image.
Point A1 is the point that has the x-coordinate equal to 2cos(360/7). Since P1 is the point at the origin, cos(360/7) can be obtained by bisecting the segment P1A1. A unit circle centered at P1 can also be constructed. Constructing a heptagon inscribed inside the unit circle centered at P1 should be easy, now that we can obtain a segment equal to cos(360/7).
I also want to add that the hyperbola can be generated by GeoGebra if you know 5 points on the hyperbola. In my trisection post I mentioned that an infinite number of points can be generated using the Hyperbola Secant Theorem. The asymptote lines, point P0 and the Hyperbola Secant Theorem can be used to generate 4 additional points.
Nonagon
In a future post I will try to show a similar construction for the nonagon. The cubic equation that can be used for the nonagon is 4x3 – 3x – 0.5. This cubic equation is usually discussed in connection with trisecting a 60 degrees angles since one of the roots is cos(20). But one of the roots is -cos(360/9)=-cos(40). Cos(40) can be used to construct a nonagon inscribed in a unit circle.
There is a high chance that the real roots of all third degree polynomials can be solved in a similar way using the intersection of Lill’s circles and rectangular hyperbolas that have the x-axis as one of the asymptote lines.

2 comments